А вот нечего чрезмерно тренировать слух, чтобы коробило от разницы в 8 центов...А если оркестр настраивается на 442 Гц, но рояль остается в привычном строе 440Гц, компромисс усугубляется )))
Почему частоты нот строятся от ля? (1 онлайн
- Автор темы GregH
- Дата начала
Вы используете устаревший браузер. Этот и другие сайты могут отображаться в нём некорректно.
Вам необходимо обновить браузер или попробовать использовать другой.
Вам необходимо обновить браузер или попробовать использовать другой.
Последнее редактирование:
На самом деле возникла потребность на протяжении одного сочинения уходить из одного лада в другие, сначала «соседние», а потом и дальние. Иначе долгую музыкальную мысль (длинную музыкальную волю, если угодно) не выразишь. Можете себе представить, каково слушать даже небольшую симфонию (минут 15-20), целиком написанную в одном ладу? Масштаб изменился. Вместо куплетной формы (100500 раз примерно одно и то же) захотелось разненького.
Да, это так. Но в квинтовом строе для перехода из лада C-dur в лад E-mol достаточно F заменить на F#. А для перехода из
С-dur в A-mol необходимо понизить ступень D на комму (D↑). Это только в РТС12 До-мажор и Ля минор располагаются на одних и тех же ступенях.
В подавляющем большинстве музыкальных произведений используется от 7 до 12 ступеней. И этого набора ступеней обычно хватает для перехода в родственные лады. То есть 12 клавиш вполне достаточно для реализации сложного музыкального образа, выходящего за пределы одного диатонического лада. Проблемы лишь в том, чтобы в рамках базового лада и в ходе транспонирования сохранялась акустическая чистота воспроизводимых интервалов: квинт, терций, секунд и даже тритона.
В РТС12 это невозможно по определению из-за "ненатуральных" пропорций терций.
В квинтовом строе это возможно, но только при правильном понимании структуры квинтового лада, в котором интервалы с пропорцией с пятеркой в числителе или знаменателе рождаются, начиная с восьмого квинтового шага, а не на четвертом и пятом квинтовых шагах.
Все музыканты уверены, что квинта больше кварты, большая терция больше малой терции, а целый тон больше ум. тона.
Давайте возьмем в качестве примера октаву А3 - А4 (220 Гц - 440 гц).
Поделим эту октаву ровно пополам и получим ступень с частотой 330 Гц, это - Е4. Шаг между Е4 и А3 равен 110 Гц и шаг между А4 и Е4 также равен 110 Гц. Но А3 - Е4 - это квинта, а Е4 - А4 - это кварта, они же не должны быть равны ?
Оказывается, равенство частотных шагов вовсе не означает равенства интервалов.
Частотный шаг А3 - Е4 дает прирост высоты звука на 110 Гц, а пропорция музыкального интервала А3 - Е4 выражается натуральной дробью 330/220 = 3/2.
Частотный шаг Е4 - А4 дает прирост высоты звука на те же 110 Гц, но пропорция музыкального интервала Е4 - А4 выражается натуральной дробью 440/330 = 4/3.
То есть, в интервальном выражении нижняя квинта больше верхней кварты, но в частотном измерении нижняя квинта равна верхней кварте:
220(А3)----------330(Е4)----------440(А4)
Е4 = (А3 + А4)/2 = (220 Гц + 440 Гц)/2 = 660 Гц/2 = 330 Гц.
Точно также частотный шаг в большую терцию А3 -- С# равен частотному шагу в малую терцию C#4 -- Е4
220(А3)----------275(C#4)----------330(Е4)
Ступень C#4 делит квинту А3 - Е4 строго пополам.
C#4 = (А3 + Е4)/2 = (220 Гц + 330 Гц)/2 = 550 Гц/2 = 275 Гц.
Более того, частотный шаг в целый тон А3 -- B3 равен частотному шагу в ум. тон B3 -- C#4
220(А3)-------247,5(В3)-------275(C#4)
Ступень В3 делит б.терцию А3 - C#4 строго пополам.
B3 = (А3 + C#4)/2 = (220 Гц + 275 Гц)/2 = 247,5 Гц.
Базовые интервалы мажорной гаммы A-dur наглядно демонстрируют нам торжество частотной симметрии, которая формирует важнейший акустический признак тонального родства опорных ступеней мажорной гаммы - однородный комбинационный тон A.
Аналогично, в натуральной гамме До-мажор ступень G4 делит октаву С4 - С5 строго пополам по частоте, ступень Е4 делит строго пополам квинту С4 - G4, а ступень D4 делит строго пополам б.терцию С4 - Е4. И у всех этих интервалов комбинационный тон октавно кратен тону С.
В равномерной темперации тональная симметрия нарушена: незначительно в паре квинта-кварта и очень явно в паре б.терция-малая терция.
Давайте возьмем в качестве примера октаву А3 - А4 (220 Гц - 440 гц).
Поделим эту октаву ровно пополам и получим ступень с частотой 330 Гц, это - Е4. Шаг между Е4 и А3 равен 110 Гц и шаг между А4 и Е4 также равен 110 Гц. Но А3 - Е4 - это квинта, а Е4 - А4 - это кварта, они же не должны быть равны ?
Оказывается, равенство частотных шагов вовсе не означает равенства интервалов.
Частотный шаг А3 - Е4 дает прирост высоты звука на 110 Гц, а пропорция музыкального интервала А3 - Е4 выражается натуральной дробью 330/220 = 3/2.
Частотный шаг Е4 - А4 дает прирост высоты звука на те же 110 Гц, но пропорция музыкального интервала Е4 - А4 выражается натуральной дробью 440/330 = 4/3.
То есть, в интервальном выражении нижняя квинта больше верхней кварты, но в частотном измерении нижняя квинта равна верхней кварте:
220(А3)----------330(Е4)----------440(А4)
Е4 = (А3 + А4)/2 = (220 Гц + 440 Гц)/2 = 660 Гц/2 = 330 Гц.
Точно также частотный шаг в большую терцию А3 -- С# равен частотному шагу в малую терцию C#4 -- Е4
220(А3)----------275(C#4)----------330(Е4)
Ступень C#4 делит квинту А3 - Е4 строго пополам.
C#4 = (А3 + Е4)/2 = (220 Гц + 330 Гц)/2 = 550 Гц/2 = 275 Гц.
Более того, частотный шаг в целый тон А3 -- B3 равен частотному шагу в ум. тон B3 -- C#4
220(А3)-------247,5(В3)-------275(C#4)
Ступень В3 делит б.терцию А3 - C#4 строго пополам.
B3 = (А3 + C#4)/2 = (220 Гц + 275 Гц)/2 = 247,5 Гц.
Базовые интервалы мажорной гаммы A-dur наглядно демонстрируют нам торжество частотной симметрии, которая формирует важнейший акустический признак тонального родства опорных ступеней мажорной гаммы - однородный комбинационный тон A.
Аналогично, в натуральной гамме До-мажор ступень G4 делит октаву С4 - С5 строго пополам по частоте, ступень Е4 делит строго пополам квинту С4 - G4, а ступень D4 делит строго пополам б.терцию С4 - Е4. И у всех этих интервалов комбинационный тон октавно кратен тону С.
В равномерной темперации тональная симметрия нарушена: незначительно в паре квинта-кварта и очень явно в паре б.терция-малая терция.
возьмем для простоты струнный квартет 
вибрато, отсутствие ладов решает частично проблему ртс?
рок группа, две гитары, бас, драмс
Бенды, вибрато решают частично проблему ртс?
Вокалист же всегда немного тяготеет к натуральному строю?
я о том, что на практике проблема решена так-то
вибрато, отсутствие ладов решает частично проблему ртс?
рок группа, две гитары, бас, драмс
Бенды, вибрато решают частично проблему ртс?
Вокалист же всегда немного тяготеет к натуральному строю?
я о том, что на практике проблема решена так-то
Что вы хотите этим показать? Что безразмерная логарифмическая величина (цент) не переводится в размерную (герц)?Оказывается, равенство частотных шагов вовсе не означает равенства интервалов.
Я бы не стал искать здесь какое-то «волшебное» соотношение чисел. Эти цифры верны только для обертонового звукоряда, ибоСтупень C#4 делит квинту А3 - Е4 строго пополам.
C#4 = (А3 + Е4)/2 = (220 Гц + 330 Гц)/2 = 550 Гц/2 = 275 Гц.
в РТС-12 частоты ля-мажорного трезвучия A=220, C#=277,183 и E=329,628 (нет равной разницы), в пифагорейском (чисто квинтово-октавном) — A=220, C#=278, E=330.
А обертоновый звукоряд при базовой частоте n будет иметь последующие частичные тона 2n, 3n, 4n... и т.д.. Разумеется, разница между любыми двумя соседними членами прогрессии будет всегда n. К тому же слышим мы, человеки, соотношения частот, а не шаги в герцах.
И второе, не мной подмеченное: при исполнении мелодии (горизонталь) лучше звучит пифагорейский строй, а при построении гармонии (вертикаль) — натуральный звукоряд. А если у имярека и гармония, и мелодия, то пусть с ума сходит.
В классическом оркестре есть инструменты с фиксированной настройкой (фортепиано, арфа, ударные), а есть те, которые могут находу поправить интонацию (струнные и духовые). Если бы я писал концерт для фортепиано с оркестром, и струнные у меня вступали бы с «лирической сексты», я бы на стал дублировать терцовый тон у струнных в партии фортепиано, оставил бы квинту, а где-нибудь потом, на слабых долях дополнил бы партию до трезвучия. Пусть струнные сыграют (интуитивно!) этот терцовый тон повыше (в миноре) или пониже (в мажоре), а рояль со своей РТС-12 пусть им не мешает. Впрочем, это мои заморочки, основанные на моём опыте и на моём слухе.Но в квинтовом строе для перехода из лада C-dur в лад E-mol достаточно F заменить на F#.
Так вот, прежде чем вернуться к процитированной строке, познакомьтесь (если ещё не) с «модуляцией Колльера», обсуждалась на форуме тут. Колльер, используя несовершенство строёв, сполз на довольно большое количество центов всего за несколько гармоний. То же самое можно было повторить и на более простых гармониях, просто больше времени потребовалось бы.
А в гипотетическом концерте для фортепиано с оркестром придётся всё время обнулять это сползание, и где-то придётся не один тон «перестраивать».
Вы сравниваете абсолютные значения частот, отсюда и такие выводы. )) Вообще-то цент, согласно концепции Гарбузова, это сотая часть ПОЛУТОНА. Отклонения в пределах плюс-минус 35 центов ощущаются как неизменная высота, поскольку человеческий слух - как интонационный, так и ритмический - имеет зонную природу.чтобы коробило от разницы в 8 центов
--Вообще-то имелась в виду европейская музыка - например, Губайдулина и др.Да таких отчаянных половина населения планеты
Не совсем верно. В мажорном трезвучии А-C#-E в рамках пифагорова строя в данной позиции пропорция диеза практически равна дроби 25/24. Потому что реально ступень С здесь имеет два знака альтерации: пифагорейский диез (~20/19) и пифагорова комма (~73/74). В сумме получается диез европейского чистого строя (~25/24). Поэтому: A=220, C#=275.3, E=330. То есть частотный шаг A - C# практически равен частотному шагу C#-E. У всех трех двузвучий в рамках мажорного аккорда А-C#-E комбинационный тон октавно кратен тону А.в пифагорейском (чисто квинтово-октавном) — A=220, C#=278, E=330.
Хуже - она не имеет не только решения, но даже постановки: никто не может наверняка сказать, по каким критериям строй можно считать идеальным, т.к. сами предлагаемые критерии являются взаимоисключающими.А вообще - проблема построения идеального строя, похоже, в принципе
не имеет решения.
Плюсанул. Давно именно так себе составил мнение, но всё никак не собрался где-нибудь сформулировать.Что касается количества нот. Зависимость высоты тона от частоты логарифмическая, значит никакое равномерное деление октавы на более мелкие интервалы не позволит получить благозвучные интервалы с соотношениями частот типа 2/3, 3/4. Поэтому используется такое количество нот, при котором эти соотношения будут достаточно близки.
Попробуйте сами посчитать, в какую степень надо возвести 1.5, чтобы получилась степень двойки? Если точно, то ни в какую, но достаточно близкие значения дадут 1.5 в 12-й и 2 в 7-й. Примерно такую же, чуть более хорошую, точность дадут степени 24 и 41, заметно лучшую — 31 и 53. Но ноты размером в 1/53-ю октавы никому нафиг не упёрлись.
А по поводу "ноты размером в 1/53-ю октавы никому нафиг не упёрлись" - тут не только вопрос нахождения наименьшего (более простого) решения, а и то, что 53, кроме этих хороших попаданий, даёт так же и много мусора. А слишком много "тритонов" в гамме не нужно.
Отнюдь.прошедший сквозь тысячелетия совершенный музыкальный строй, образованный чередой чистых квинт
Строй, основанный исключительно на чистых квинтах не является и не может быть совершенным. Даже в пределах конкретной тональности.
Пифагорейский строй - лишь первая известная попытка упорядочить музыкальные интервалы, используя математический аппарат.
То есть это исторически интересный факт, кроме того, полезный для рассмотрения в первом приближении.
Музыканты веками наощупь искали совершенный строй практически вслепую. Но сегодня можно уже попытаться упорядочить все знания, полученные музыкантами прошлого эмпирическим путем, с точки зрения современных научных представлений.
Основа в данном случае - физиология. Физика и математика - только на вторых ролях.
А с точки зрения физиологии можно сформулировать два основных факта:
1. Степень консонантности созвучия пропорциональна проценту совпадающих обертонов.
2. Человеческий слух имеет разрешение примерно 0.2% (3 цента). Звуки, частоты которых менее этой границы, воспринимаются как унисон.
Понятно, что в строе, основанном на квинтах, процент совпадающих обертонов будет низким, например, для 81/64 лишь каждый 81-й обертон одной ноты будет совпадать с каждым 64-м обертоном второй. Более того, 81-й обертон от C1 имеет частоту более 21 кГц, а потому выходит за пределы звукового диапазона. Выходит, процент совпадающих обертонов в пределах звукового диапазона вообще равен нулю. Поэтому вполне естественно, что с точки зрения физиологии человеческого слуха интервалы типа 5:3 или 6:4 намного консонантнее соответствующих им интервалов на основе чистых квинт.
Последнее редактирование:
Зонная теория Гарбузова построена на песке, поскольку основывается на ответах испытуемых, не имеющих ни музыкального образования, ни музыкального опыта. Это само по себе настораживает. В музыкальной гармонии главное - не абсолютная высота тона, а звуковысотное соотношение тонов. Пропорция волчьей квинты превышает пропорцию натуральной квинты (3/2) на 23 цента. Получается по Гарбузову они одинаково благозвучны ? Дикость полная.Отклонения в пределах плюс-минус 35 центов ощущаются как неизменная высота, поскольку человеческий слух - как интонационный, так и ритмический - имеет зонную природу.
Вот, например, темперированная квинта (на фоно) всего на 2 цента уже натуральной, но даже такое малое отклонение ловит музыкальный слух из-за легкого вибрато (колебание громкости примерно раз в секунду).
если среднестатистический слушатель не ощутит явно плюсов от 31 клавиши (условно) в пьесе, то все рассуждения так и останутся в лабораторииЗонная теория Гарбузова построена на песке, поскольку основывается на ответах испытуемых, не имеющих ни музыкального образования, ни музыкального опыта. Это само по себе настораживает.
Для кого-то - возможно, спорить не буду. Но в моей личной практике нередко приходится заниматься редактированием записанного материала, в т.ч. тюнингом инструментов и вокала. Так вот, повода для несогласия с Гарбузовым у меня не возникало. ))Зонная теория Гарбузова построена на песке
Кстати, я не абсолютник (что не всегда является неоспоримым достоинством), а обычный тренированный релятивист.
И редактирую питч не по сетке (это школярство), а в зависимости от того, какой ступенью лада является конкретная нота в ДАННЫЙ момент, с учетом движения мелодии и прочих факторов.
Кстати, Холопов тоже помогает. ;-)
И по поводу базиса теории Гарбузова, основанной на опросах простолюдинов ))) - теория кривых равной громкости, в обиходе именуемых по старинке Fletcher - Munson curves, тоже базируется на опросе простых смертных, а не закоренелых профи.
Физиология одна на всех. ;-)
P.S. И ещё мне кажется, что говоря о центах, мы имеем в виду совершенно разное...
Последнее редактирование:
По поводу разных трактовок "стройности": я давно увлекаюсь этнической музыкой, общаюсь и сотрудничаю с носителями разных музыкальных культур.
Однажды я показал на форуме кое-что из своих работ, и один из комментаторов попенял мне, что "дудочки не строят".
На это один из носителей ответил в мою защиту - не слушайте эту музыку своим темперированным ухом. )))
Однажды я показал на форуме кое-что из своих работ, и один из комментаторов попенял мне, что "дудочки не строят".
На это один из носителей ответил в мою защиту - не слушайте эту музыку своим темперированным ухом. )))
Если вы знакомы с альтистом Даниловым (говорят, неплохой альтист ))) то должны помнить фразу "Ничто не слишком" ;-)А вот нечего чрезмерно тренировать слух
Прежде чем определяться с критерием идеальности музыкального строя, необходимо определиться с образом идеального двузвучия.Строй, основанный исключительно на чистых квинтах не является и не может быть совершенным. Даже в пределах конкретной тональности.
Пифагорейский строй - лишь первая известная попытка упорядочить музыкальные интервалы, используя математический аппарат.
И этот образ давно найден. Наиболее благозвучными считаются созвучия с натуральными (целочисленными) пропорциями. Чем меньше целые числа в звуковысотной пропорции, тем гармоничней данное созвучие. Октава (2/1), квинта (3/2), кварта (4/3), б.терция (5/4), м.терция (6/5), тритон (7/5), хром. б.терция (7/6), хром. м.терция (8/7), ц.тон (9/8), ум. ц. тон (10/9).... полутон (16/15), греческий диесис (256/243 = 20/19), диез чистого европейского строя (25/24).
Отсюда идеальный музыкальный строй - это такой строй в котором от любой ступени строя можно построить любой из перечисленных выше натуральных интервалов.
Так вот, квинтовый строй, получивший в Греции имя Пифагора, а в Китае название "12 люй", как раз и обладает таким качеством.
Имея в своей основе звуковысотную пропорцию 3/2, непрерывная череда квинтовых шагов уже на пятом шаге порождает пропорцию, очень близкую к 20/19 (погрешность 2 цента), на седьмом шаге - пропорцию ~16/15 ((погрешность 2 цента), на восьмом шаге - пропорцию ~8/5 и ~5/4 (погрешность 2 цента), на девятом шаге - пропорцию ~6/5 и ~5/3 (погрешность 2 цента), на десятом шаге - пропорцию ~9/5 и ~10/9 (погрешность 2 цента).
Кроме того, этот же квинтовый ход порождает звуковысотные пропорции с семеркой в числителе или в знаменателе.
Да как бы не считаются (кем-то), а всё это дано природой.И этот образ давно найден. Наиболее благозвучными считаются созвучия с натуральными (целочисленными) пропорциями.
Но ноты размером в 1/53-ю октавы никому нафиг не упёрлись.
А септимы и секунды это (случайно-внезапно) не мусор по сравнению с терциями и квинтами в диатонической системе?а и то, что 53, кроме этих хороших попаданий, даёт так же и много мусора.
Противопоставляю два тезиса. В абсолютно любой ладо-гармонической системе, от самых примитивных до самых авангардных, должны противопоставляться более и менее благозвучные интервалы. Напряжение — разрешение, вдох — выдох, подняли ногу — опустили (сделали шаг). Так мы живём и по этому же закону мы организовываем музыкальную ткань. Не могут существовать только благостные интервалы — слух тут же (в историческом масштабе «тут же») выделит из них самый благостный и противопоставит ему менее благостный.
Если посмотреть музыкальную культуру с совсем архаичных времён, то начиналась она с совсем простых ладов — из двух или трёх тонов. И устоем (в двух-или многоголосии) долгое время считался только унисон. Постепенно (не линейно и не синхронно в разных культурах) осваивался обертоновый звукоряд, и устоем могла быть кварта или квинта. Затем большая терция получила возможность заканчивать пьесу. А малая — нет. Сколько минорных пьес заканчивалось мажорным трезвучием, и не потому, что автор хотел дать надежду слушателю хотя бы в конце своего опуса (это побочный эффект), а потому что минорное окончание слышалось неустойчивым.
В профессиональной (не народной) музыке освоение натурального ряда шло дальше. Любителей джаза или поклонников Дебюсси невозможно напугать нагромождением септим, секунд и тритонов. Скрябин свою дорогу проложил — к Вышнеградскому, например. У него
в позднем творчестве очень много «колких и хрупких» кварто-тритоновых образований, а у Вынеградского эта хрупкость поднята ещё на этаж системой EDO-24, в которой вообще нет гармонических (целочисленных) интервалов. EDO-24 это как бы EDO-12 на максималках. (Тут
в Сравнительном слушании давал Прелюдию ля-минор Скрябина и прелюдию Вынеградского, попробуйте услышать родство.)
Пауль Хиндемит свою систему предложил — не мажор и не минор, в его Ludus Tonalis только 12 прелюдий и фуг (а не 24).
Системы становятся всё более авторскими, да. Но иерархический принцип (вот это более благозвучно, а это менее) никуда никогда не исчезал.
С системами 31- и 53-EDO то же самое. (Почти, объясню ниже.) Точно так же музыкальная ткань, созданная в этих системах, имеет свои напряжения и разрешения, и их можно проживать как что-то интересное (проживать эмоционально, если угодно). В них можно жить ничуть не хуже, чем в 12-EDO.
Сложность восприятия этих систем в другом. Пишу по памяти, но в 53-й системе, кажется, только разных прилично звучащих секст шесть штук. Гармонически они совсем высоко в обертоновом ряде, и для их различения, да, требуется неплохой от природы и тренированный биографией слух. Но и удовольствие художника другое, когда у тебя так много интервальных красок. Как много разного можно различить! Господь Бог когда-то давно уже издал указ людям — давать вещам свои имена. Вот это ровно оно: для каждого движения души больше чуткости, больше интервалов, больше различения. Так что движение в сторону EDO-19, 31, 53 — вполне по заповедям.
По поводу слова «почти». Поднимаясь до шести секст мы упираемся в человеческие пределы восприятия. Разницу между интервалами всё труднее улавливать. Наша привычная (не лучшая, не худшая, а просто привычная) ощутимо дискретная система из совершенных и несовершенных консонансов и диссонансов превращается в хрому (это термин). Дальше вверх идти, в общем, и незачем.
Я сам не занимаюсь этими системами. Но был опыт участия в репетициях и двух представлениях оперы, написанной в EDO-31 (можно поискать по форуму по имени Кайл Гэнн, Kyle Gann). Какое-никакое, а погружение. После двухнедельного пребывания в такой музыке я несколько месяцев не мог избавиться от ощущения грязи всего, звучащего вокруг. И только деньги заставили меня заткнуть уши тампонами и приступить к привычным оркестровкам. Только деньги.
Да, читатели, вы не можете принести такую музыку в массы, но вы можете взять это для себя, а, если повезёт, то и поделиться с друзьями. Тут уж хозяин барин, как решит, так и будет.
Я не знаю, позволяют ли правила форума положить хер на среднестатистического слушателя. Я бы положил, если бы было можно. Среднестатистического слушателя (в вакууме, нет?) лучше держать в поле зрения — он умеет материться, плеваться, кидаться камнями. Но не более того.если среднестатистический слушатель не ощутит явно плюсов от 31 клавиши (условно) в пьесе, то все рассуждения так и останутся в лаборатории
Всё придуманное пришло из лабораторий, чтобы под ними не понимать. Не всё было принято массами, но всё же. Пифагорейски измерения струн, все эти Боэции из поздней античности — лаборатория. МММ возрождения — месса, мадригал, мотет. Монахи в монастырях, их попытки наполнить музыку своими собственными приёмами развития (а то она всё за текстом следовала и принимала его форму) — чем не многовековая лаборатория? Позже — фуга, одна из высших музыкальных форм, вовсе не гребенщиковыми того времени была придумана. В Новое время — сонатная форма (диалектика в музыке). Далее везде...
вот вотВсё придуманное пришло из лабораторий, чтобы под ними не понимать. Не всё было принято массами, но всё же.
Вы про источник знаний, а я именно про востребованность знаний
пока видится, что перехода от ртс куда-то дальше не прогнозируется, но наблюдать интересно
вспомнилось выражение - широкая востребованность в узких кругах
А септимы и секунды это (случайно-внезапно) не мусор по сравнению с терциями и квинтами в диатонической системе?
Верно. Диссонансы есть и тут, большинству их хватает для создания этого самого контраста: "Напряжение — разрешение, вдох — выдох, подняли ногу — опустили".
Вы выше много написали про "положить хер на среднестатистического слушателя" и прочую элитарность, но я же не ставил оценку, какая система лучше, а какая хуже, я отвечал на вопрос "почему так вышло, что ступеней 12".
Кстати, может кто в курсе, в альбоме Pink Floyd Atom heart mother в первой композиции не использовались какие-то эксперименты, расширяющие звукоряд? Просто там есть ощущение фальши, но какой-то уж очень красивой, особенно когда духовые звучат.
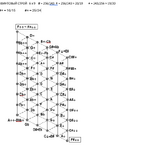
Выкладываю диаграмму полного квинтового строя, в которой роль диезно-бемольной альтерации выполняет греческая лимма #=256/243 (диесис), а роль тонкой альтерации выполняет пифагорова комма ↑ = 74/73, Данный строй замкнут - на 54 квинтовом шаге мы возвращаемся в точку старта. В трехмерном представлении квинтовый строй - это тороидальная замкнутая спираль. У такой структурной модели в качестве центра может быть выбрана любая ступень.
Вложения
А всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфереВ трехмерном представлении квинтовый строй - это тороидальная замкнутая спираль. У такой структурной модели в качестве центра может быть выбрана любая ступень.
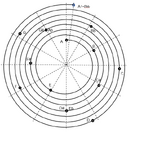
Если октавный шаг уподобить одному круговому витку, то 12 ступеней пифагорова строя от А (они же 12 люй) будут располагаться на многовитковой спирали. В том числе - ступени натуральной гаммы С-Dur и E-mol с акустически чистыми терциями.
Именно E-mol, а не A-mol.
С учетом октавной коррекции, 12 ступеней разместятся на одном витке окружности, наподобие часового циферблата.
В китайской традиции 12 ступеней музыкального лада 12 люй делят окружность на 12 неравных частей, которые уподобляются 12 месяцам солнечного года.
Большой месяц на диаграмме - греческая апотома с пропорцией ~16/15, а малый месяц - греческая лимма с пропорцией ~20/19.
Семь малых месяцев (полутонов) и пять больших формируют два музыкальных лада.
Мажорный лад C-Dur включает в себя три чистых мажорных трезвучия и два минорных.
Минорный лад E-mol включает три чистых минорных трезвучия и два мажорных.
Для транспозиции достаточно еще одного квинтового шага (вперед или назад).
Именно E-mol, а не A-mol.
С учетом октавной коррекции, 12 ступеней разместятся на одном витке окружности, наподобие часового циферблата.
В китайской традиции 12 ступеней музыкального лада 12 люй делят окружность на 12 неравных частей, которые уподобляются 12 месяцам солнечного года.
Большой месяц на диаграмме - греческая апотома с пропорцией ~16/15, а малый месяц - греческая лимма с пропорцией ~20/19.
Семь малых месяцев (полутонов) и пять больших формируют два музыкальных лада.
Мажорный лад C-Dur включает в себя три чистых мажорных трезвучия и два минорных.
Минорный лад E-mol включает три чистых минорных трезвучия и два мажорных.
Для транспозиции достаточно еще одного квинтового шага (вперед или назад).
Вложения
Сейчас просматривают
Всего: 2 (пользователей: 0, гостей: 2)